
現在では自分の知りたい年月日を指定すれば曜日が分かる便利なウェブサイトも多いが,西暦と年月日を代入すればその日が何曜日であったかを計算で求めることができる公式があるのをご存じだろうか?ドイツの数学者クリスティアン・ツェラーが考案した「ツェラーの公式」と呼ばれる公式だ。
y年m月d日の曜日Dは次のツェラーの公式で導くことができる。(ただし,1月と2月はそれぞれ前年の13月,14月とする。)

これはツェラーの公式の変形だが,ここまで複雑なのは閏(うるう)年が4年に1度あること,西暦年が100の倍数であれば閏年がないこと,しかし西暦年が400の倍数なら閏年を導入することなどグレゴリオ暦による取り決めなどが関係している。
ともあれ,このツェラーの公式を解くことで1なら月曜日,2なら火曜日・・・7なら日曜日のように数字に対応した曜日が導出される。
この式について,いくつか補足しておこう。公式中にある変数CとYはそれぞれ以下の式で求める。
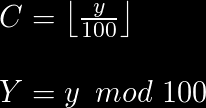
このCとYは西暦上2桁と下2桁を表すもので,1950年であればCは「19」,Yは「50」となる。
また,記号”⌊ ⌋”は床関数を表すもので,⌊x⌋であれば実数x以下の最大の整数という意味だ。例えば⌊2.3⌋なら2,⌊54.9⌋なら54になる。 公式中の第2項目において,分母の「10」と分子の「26」が約分されていないのは床関数の計算を簡単にするためのものだ。
公式中の”mod7”や”mod100”は,それぞれ「7で割った余り」,「100で割った余り」を意味する。
では,実際に2017年1月31日が何曜日であるか計算して求めてみよう。
ここで注意しなければならないのは,上記にもある通り”1月”と”2月”はそれぞれ前年の”13月”と”14月”として扱わなければならないので「2017年1月31日」は「2016年13月31日」として計算するのだ。つまり,変数にはy=2016,m=13,d=31が代入される。
変数Cは西暦の上2桁の数字を表している。
Cを求める式から計算するとC=⌊y/100⌋なので,yに2016を代入してC=⌊2016/100⌋=⌊20.16⌋=20となり西暦の上2桁が導出される。
同様に,変数Yは西暦の下2桁の数字を表している。Yを求める式から計算するとY=y mod 100なので,yに2016を代入して100で割った余り,Y=2016 mod 100=16となり西暦の下2桁が導出される。
それぞれの変数を代入してD=[{31+⌊26(13+1)/10⌋+16+4-40+5+5}mod 7]+1となる。
計算の優先順位に影響のないように式を整理してD=[(31+⌊26*14/10⌋-10) mod 7]+1D=[(31+⌊364/10⌋-10) mod 7]+1D=[(31+36-10) mod 7]+1D=(57 mod 7)+157を7で割った余りは1なのでD=1+1=22017年1月31日の曜日は2に対応した曜日である火曜日だ。
ツェラーの公式で曜日を求めるにはグレゴリオ暦かユリウス暦かを判断しておかなければならない。例えばユリウス暦からグレゴリオ暦にいち早く切り替わった国では1582年10月4日(ユリウス暦)の翌日は1582年10月15日となっているため,調べたい年月日がユリウス暦である場合には上記のツェラーの公式は使えないため注意が必要だ。
