円周率上にある奇妙な「ファインマン・ポイント」とは？

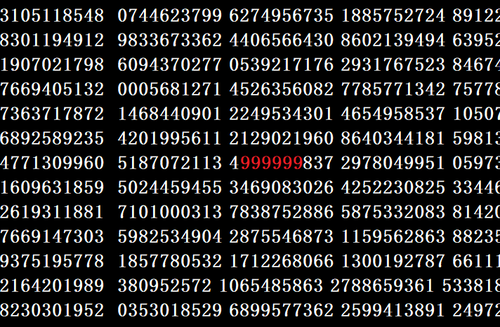
円周を直径で割ることによって得られる3.14159265･･･と無限に続く円周率。この円周率上の小数点以下762桁目から767桁目には「9」が6つ連続した奇妙な部分が存在する。かつて,アメリカの物理学者であるリチャード･ファインマンがこの部分まで暗唱し,ここまで覚えておきたいと講義中に述べたことからこの部分はファインマン･ポイントと呼ばれている。
ここまで早く6つの連続した数字が並ぶのは実は珍しい。例えば,4桁の数字が最初に連続して並ぶのは4,751桁目からの「8」であり,5桁の数字が最初に連続して並ぶのは17,534桁目からの「0」である。

また,各数字において6桁の数字が連続して並ぶ小数点以下の桁数は以下のようになっている。

000000・・・169万9927桁目
111111・・・25万5945桁目
222222・・・96万3024桁目
333333・・・71万100桁目
444444・・・82万8499桁目
555555・・・24万4453桁目
666666・・・25万2499桁目
777777・・・39万9579桁目
888888・・・22万2299桁目
999999・・・ 762桁目

ファインマン・ポイントは他の数字よりも3桁程も小さい。乱数によって生成した数字列ではこれほど早く6桁の数字が並ぶ確率はなんと0.08％しかないのだ。さらに,次に6つの数字が連続して並ぶのはまたしても「9」であり,19万3034桁目から始まっている。いわば”第二のファインマン・ポイント”も存在しているのだ。
円周率は0から9までの数字がほとんど均等に出現することが知られており,このファインマン・ポイントも単なる確率的なものに過ぎないのかもしれないが奇妙である一方で,大変興味深くもある。